Nous allons réaliser une résolution d'un exercice et ainsi montrer la présence de centre, axes, plans de symétrie dans les mathématiques

Nous avons comme exemple le tétraèdre régulier.

G isobarycentre de A, B, C, D. Où se situe G ?

Comme G est le barycentre de (A;1) (B;1) (C;1) (D;1), on a :

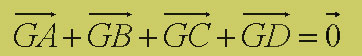
d'où :

G est le barycentre de (A;1) (B;1) (C;1) (D;1), donc du tétraèdre.

Prenons I milieu de [AB], J milieu de [CD]. D'après le théorème d'associativité du barycentre on a :

G barycentre de (I;2) (J;2), donc G est le milieu de [IJ].

On a la même démonstration pour G milieu de [KL], et G milieu de [MN].

Les droites (IJ), (KL), (MN) sont concourantes en G.

[IJ] et [KL] ont le même milieu, donc IKJL est un parallélogramme. On a alors ici un plan médiateur.

G appartient à ce plan, puisque G est le milieu du parallélogramme IKJL et donc le milieu de ces diagonales, qui se coupent en leur milieu.

On a donc IG = JG = KG = LG.

D'où

GA = GB = GC = GD

G est donc le centre de symétrie du tétraèdre.

Nous avons aussi :

Le plan médiateur P1 de [AC], passe par le point B.

On a alors un plan de symétrie du tétraèdre.

On remarque aussi que G1, centre de gravité du triangle ADC, appartient à ce plan. Car G1 se trouve au centre du triangle ADC.

Il en est de même pour chaque sommet et triangle associé.

Axes de symétrie :

H est le centre de gravité du triangle CDB, avec H barycentre de (D;1) (B;1) (C;1).

G appartient à (AH) en effet G barycentre de (A;1) (B;1) (C;1) (D;1)

Donc G barycentre de (A;1) (H;3). On a alors A;G;H alignés.

Ainsi (AH) est un axe de symétrie du tétraèdre.

De même pour chaque hauteur du tétraèdre qui sont des axes de symétrie de ce dernier.